"""
Ivana Babic, Djurdjica Blazevic
"""
|
|
# ODJ prvog reda s konstantnim koeficijentima
|
|
x=var('x')
|
|
y=function('y',x)
|
|
f=desolve(diff(y,x) + y - 1,y); f
(c + e^x)*e^(-x) |
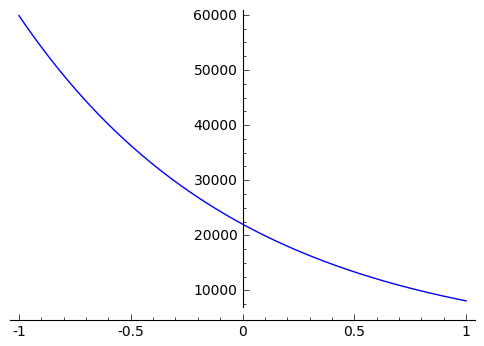
f1=desolve(diff(y,x)+y-1,y,ics=[10,2]); f1 #[x0,y(x0)]
(e^10 + e^x)*e^(-x) |
plot(f1)
|
|
# ODJ drugog reda s konstantnim koeficijentima
|
|
f2=diff(y,x,2)-y == x
|
|
desolve(f2,y)
k1*e^x + k2*e^(-x) - x |
f3=desolve(f2,y,[10,2,1]); f3 #[x0,y(x0),y'(x0)]
-x + 5*e^(-x + 10) + 7*e^(x - 10) |
f3(x=10)
2 |
diff(f3,x)(x=10)
1 |
f4=diff(y,x,2) + y == 0
|
|
desolve(f4, y)
k1*sin(x) + k2*cos(x) |
desolve(f4, y, [0,1,pi/2,4]) #[x0,y(x0),x1,y(x1)]
4*sin(x) + cos(x) |
desolve(diff(y,x,2)+2*diff(y,x)+y == 0,y,[0,3,1],show_method=True)
[(4*x + 3)*e^(-x), 'constcoeff'] |
# ODJ prvog reda (numerički pomoću Runge-Kutta metode)
|
|
x,y=var('x y')
|
|
desolve_rk4(x*y*(2-y),y,ics=[0,1],end_points=1,step=0.2)
[[0, 1], [0.2, 1.0199966672], [0.4, 1.07982711491], [0.6, 1.17807507991], [0.8, 1.30949750667], [1.0, 1.46210402431]] |
P=desolve_rk4(y*(2-y),y,ics=[0,.1],ivar=x,output='slope_field',end_points=[-4,6],thickness=3); show (P)
Warning: divide by zero encountered in divide Warning: invalid value encountered in multiply Warning: invalid value encountered in multiply Warning: divide by zero encountered in divide Warning: invalid value encountered in multiply Warning: invalid value encountered in multiply |
# ODJ prvog reda (numerički pomoću Eulerove metode)
|
|
x,y = PolynomialRing(QQ,2,"xy").gens()
|
|
eu1=eulers_method(5*x+y-5,0,1,1/2,1); eu1
x y h*f(x,y)
0 1 -2
1/2 -1 -7/4
1 -11/4 -11/8
|
eu2=eulers_method(5*x+y-5,0,1,1/2,1,algorithm="none"); eu2
[[0, 1], [1/2, -1], [1, -11/4], [3/2, -33/8]] |
p1=list_plot(eu2)
|
|
p2=line(eu2)
|
|
(p1+p2).show()
|
|
# Sustav ODJ prvog reda
|
|
t=var('t')
|
|
x=function('x',t)
|
|
y=function('y',t)
|
|
jed1=diff(x,t)+y-1==0; jed2=diff(y,t)-x+1==0
|
|
desolve_system([jed1,jed2],[x,y])
[x(t) == (x(0) - 1)*cos(t) - (y(0) - 1)*sin(t) + 1, y(t) == (x(0) - 1)*sin(t) + (y(0) - 1)*cos(t) + 1] |
jed3=desolve_system([jed1, jed2], [x,y], ics=[0,1,2]); jed3
[x(t) == -sin(t) + 1, y(t) == cos(t) + 1] |
jedx,jedy=jed3[0].rhs(),jed3[1].rhs()
|
|
plot([jedx,jedy],(0,1))
|
|
# Sustav ODJ prvog reda (numerički)
|
|
x,y=var('x,y')
|
|
f=[x*(1-y),-y*(1-x)]
|
|
sol=desolve_odeint(f,[0.5,2],srange(0,10,0.1),[x,y]);
|
|
p=line(zip(sol[:,0],sol[:,1]))
|
|
p.show()
|
|
# Sustav ODJ prvog reda (numerički pomoću Runge - Kutta)
|
|
x,y,t=var('x y t')
|
|
sust1=desolve_system_rk4([x*(1-y),-y*(1-x)],[x,y],ics=[0,0.5,2],ivar=t,end_points=20)
|
|
Q=[ [i,j] for i,j,k in sust1]
|
|
LP=list_plot(Q)
|
|
Q=[ [j,k] for i,j,k in sust1]
|
|
LP=list_plot(Q)
|
|
LP
|
|
# Sustav ODJ dvije jednadžbe prvog reda (numerički pomoću Eulerove metode)
|
|
t, x, y = PolynomialRing(QQ,3,"txy").gens()
|
|
f = x+y+t; g = x-y
|
|
eulers_method_2x2(f,g, 0, 0, 0, 1/3, 1,algorithm="none") #(f,g,t0,x0,y0,h,t1)
[[0, 0, 0], [1/3, 0, 0], [2/3, 1/9, 0], [1, 10/27, 1/27], [4/3, 68/81, 4/27]] |
P = eulers_method_2x2_plot(f,g, 0.0, 0.75, 0.0, 0.1, 1.0)
|
|
# Rješenje
|
|
P[0].show()
|
|

.png)
.png)
.png)
.png)
.png)
.png)